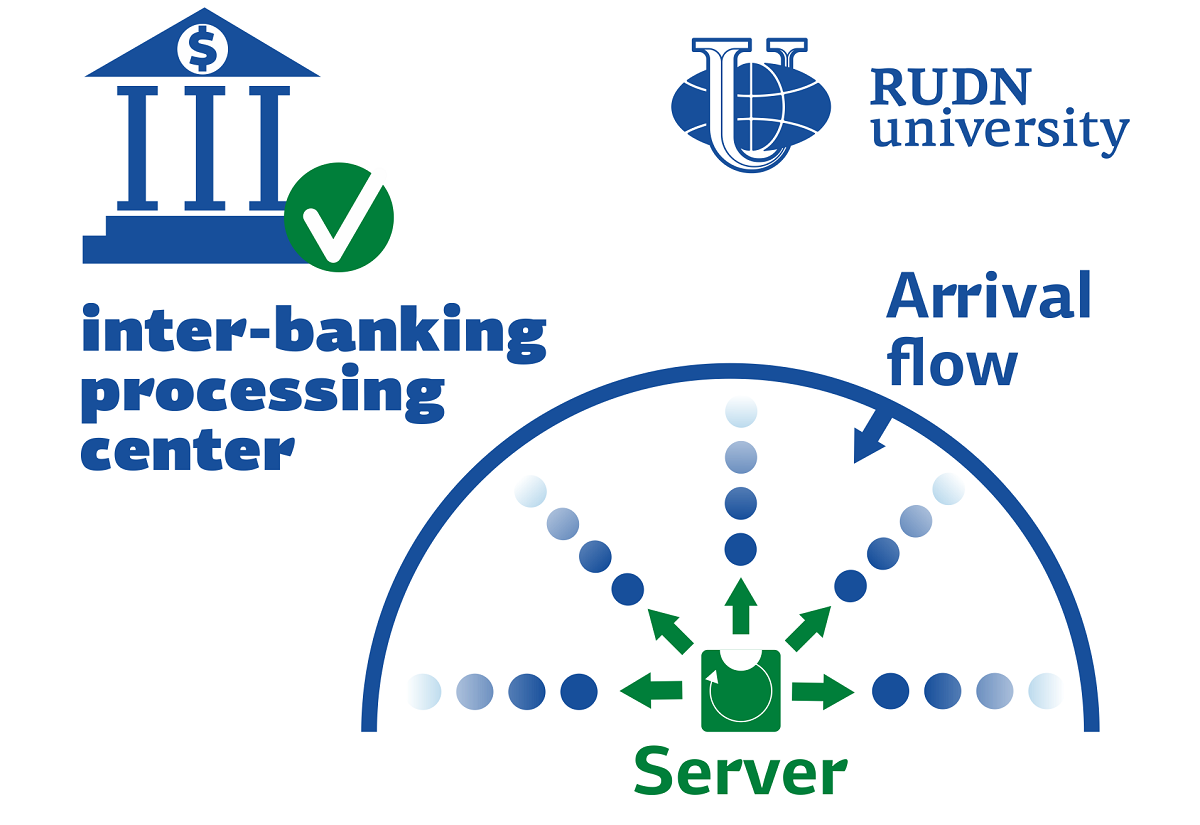
Математики 网上买足彩的app,足彩app哪个是正规的 создали модель для межбанковского процессингового центра
Система типа «поллинг» — это математическая модель, в которой один исполнитель (или сервер) по очереди выполняет несколько запросов от разных пользователей. Ее применяют в телекоммуникациях, организации производства, управлении дорожным движением и других областях. Изначально модель придумали для описания работы ремонтника оборудования на производстве. Обычно в таких моделях предполагается «нетерпеливый клиент» — это означает, что если заявка не обрабатывается в течение некоторого времени, то она покидает очередь. Математики 网上买足彩的app,足彩app哪个是正规的 предложили новый подход к поллинг-системам. В нем попавшая на обслуживание заявка не может его прервать, пока не будет обработана. На практике это реализуется, например, в банковском деле.
«В некоторых системах клиенты „абсолютно терпеливы“ и выходят из системы только после получения услуги. Наша модель возникла в ходе выполнения прикладных исследований по оптимизации работы межбанковского процессингового центра Республики Беларусь, который обрабатывает все денежные операции между банками. Специфика межбанковского процессингового центра такова, что любая финансовая транзакция, принятая для обработки в центре, должна быть реализована и за вершена», — доктор физико-математических наук, Александр Дудин, заведующий научным центром прикладного вероятностного анализа 网上买足彩的app,足彩app哪个是正规的.
В модели, предложенной математиками 网上买足彩的app,足彩app哪个是正规的, заявки поступают в систему по принципу марковского процесса — количество новых заявок не зависит от того, сколько их было в предыдущие моменты времени. После поступления, новые заявки попадают в «зал ожидания» — буфер. Предполагается, что сервер чередует работу и отдых. Время работы сервера ограничено. Если заявок в системе нет, то начинается период отдыха. При этом если время работы истекло, но обработка заявки не закончилась, сервер не может уйти на отдых. Длительность «отпуска» и работы распределена по фазовому закону, который существенно более общий, чем популярный в литературе экспоненциальный закон.
Математики 网上买足彩的app,足彩app哪个是正规的 исследовали полученную модель и определили условия ее устойчивости, а также определили формулы для расчета основных показателей системы — времени ожидания, вероятности, что новая заявка попадет на время отдыха сервера и т.д.
«Наша модель построена при довольно общих предположениях о вероятностных распределениях, описывающих поведение системы, и реалистичном предположении, что во многих системах текущее обслуживание нельзя прервать. Мы получили условия устойчивой работы системы и стационарные распределения состояний системы и времени ожидания. Это интересно с точки зрения применения результатов рассматриваемой модели к анализу систем типа поллинг», — доктор физико-математических наук, Александр Дудин, заведующий научным центром прикладного вероятностного анализа 网上买足彩的app,足彩app哪个是正规的.
Исследование опубликовано в Mathematics.
Аспирантка кафедры фармацевтической и токсикологической химии 网上买足彩的app,足彩app哪个是正规的 Екатерина Кузьмина успешно защитила кандидатскую диссертацию, посвящённую инновационному способу улучшения свойств уже существующих лекарств. Её исследование предлагает не создавать новые молекулы с нуля, а модифицировать уже существующие препараты с помощью механической активации лекарственной субстанции.
В профессиональный праздник стоматологов сообщаем хорошую новость: впервые в России и странах СНГ утверждён отечественный национальный стандарт (ГОСТ), регламентирующий метод определения абразивности зубных паст. За основу стандарта взята разработанная в 网上买足彩的app,足彩app哪个是正规的 методика оценки РИА — Российского индекса абразивности.
В честь Дня российской науки рассказываем о ведущих и молодых учёных 网上买足彩的app,足彩app哪个是正规的, а также о перспективных студентах, которые делают первые успехи в исследованиях. Каждому герою мы дали поделиться в цитатах результатами своих работ и значением науки в жизни. Ведущие и молодые ученые в этой статье — получатели ежегодной премии 网上买足彩的app,足彩app哪个是正规的 в области науки и инноваций. Торжественное награждение состоится на расширенном заседании ученого совета университета 16 февраля.